深度学习pytorch基础入门

1.一些技巧：

1.基础准备

库是记不完的

"""基础学习"""
"""基础学习"""
import torch
"""调用torch库"""     #深度学习的库
import numpy as np   #数学计算的库
import os            #管理文件的库
import pandas as pd  #统计的库
from IPython import display #显示的库
from d2l import torch as d2l #学习的库
import matplotlib_inline #画图的库
from torch.distributions import multinomial
"""从手电筒的分配库里面调出多项式的函数 ^-^"""
"""调用torch库"""

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
"""调用gpu，注意gpu序号"""
print(torch.cuda.is_available())
"""这里看看是否输出为true，true的话说明环境没问题"""

2.节省内存

这里先给出一个例子：

x=torch.arange(12)
x=x.reshape(3,4)
y=torch.randn(3,4)
print(id(y))
y=x+y
print(id(y))

这里会发现，两个y的地址不一样，后面的y数值并不是直接覆盖上去的，小程序没啥问题，大程序两下就把电脑搞死了。

z=torch.zeros_like(y)
z[:]=x+y
print(id(z))

这里发现，z的地址就是y的地址，当然节省地址的写法很多，如下

y[:]=y+x
x += y

3.转换成其他python对象

numpy和torch的tensor类型可以互相转换，注意转换后不共享内存，不同类型的不可以运算。

a=x.numpy()
#转换成numpy格式的张量
print(a)
x1=np.random.rand(3,4)
print(x1+a)
x2=torch.tensor(x1)
#这里将一个numpy的array格式的转换为tensor类型
print(x2.type())

4.数据集的创建与读取

import os
import pandas as pd

os.makedirs(os.path.join('..','data'),exist_ok=True)
"""
这里注意一下os.path.joint函数的用法：
os.path.joint('aaa','abc','yyy')
aaa中举一个例子 D:\\folder_name1\\folder_name2
abc这个文件下的具体文件名字：例如name.jpg,data,作用是返回一个可以访问的路径
os.makedirs:创建folder,后面的是权限模式
os.path.joint没有文件会创建文件
"""
data_file=os.path.join('..','data','house_tiny.csv')
with open(data_file,'w') as f:
    """注意学习这里的with用法"""
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每⾏表⽰⼀个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')
data=pd.read_csv(data_file)
print(data)
"""处理缺失值"""
inputs,outputs=data.iloc[:,0:2],data.iloc[:,2]
print(inputs)
inputs=inputs.fillna(inputs.mean())
"""上面这句话的意思是用inputs.mean去填补input中nall的部分"""
print(inputs)
inputs=pd.get_dummies(inputs,dummy_na=1)
""" 对于结果中的值，将原来pave替换为1，nalll替换为0，如果dummy_na=0,输出仅有alley_pave"""
print('signal:',inputs)
"""上述操作是为了一个目的，为了能够将读取的文档转为张量进行输入，因此有"""
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(X)
print(y)


"""
dummy_na=0输出为：
    NumRooms  Alley_Pave
0       3.0           1
1       2.0           0
2       4.0           0
3       3.0           0
dummy_na=1输出为：
    NumRooms  Alley_Pave  Alley_nan
0       3.0           1          0
1       2.0           0          1
2       4.0           0          1
3       3.0           0          1
"""

5.线性代数

这一部分和numpy很像，如果熟悉numpy的话这一份算简单，注意一些事情

torch.mul()是矩阵的点乘，即对应的位相乘，要求shape一样, 返回的还是个矩阵
torch.mm()是矩阵正常的矩阵相乘，（a, b）* ( b, c ) = ( a, c )
torch.dot()类似于mul()，它是向量(即只能是一维的张量)的对应位相乘再求和，返回一个tensor数值
torch.mv()是矩阵和向量相乘，类似于torch.mm()
注意区别，对应不同情况进行调用

这里给出一些简单的计算的代码，用的话还是得根据需求进行查

x = torch.arange(4)
print(len(x),x.shape)
A = torch.arange(20).reshape(5, 4)
print(A,A.T)
X = torch.arange(24).reshape(2, 3, 4)
print(X)
"""注意这是个几维的玩意"""
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存，将A的⼀个副本分配给B
A_sum_axis0 = A.sum(axis=0)
"""改变01来获得按行加和按列加"""
print(A_sum_axis0)
a=torch.tensor([[1,2,3,4,5,6]])
b=torch.arange(6).T
print(torch.mv(a,b))
"""这个是矩阵乘法，注意维度"""
"""矩阵的范数"""
u = torch.tensor([3.0, -4.0])
print(torch.norm(u))
print(torch.abs(u).sum())
print(torch.norm(torch.ones((4, 9))))

6.微分

对于计算机来说，求微分的方法为：

$f'(x)=\frac{f(x+h)-f(x)}{h}\\ 精度高一些为：\\ f'(x)=\frac{f(x+h)-f(x-h)}{2h}$

代码实现为：

def f(x):
    return 3*x**2-4*x

def numerical_lim(f,x,h):
    return (f(x+h)-f(x-h))/(2*h)
h=0.1
for i in range(5):
    print(f'h={h:.5f},numerical limit={numerical_lim(f,1,h):.5f}')
    h*=0.1
    
"""学习绘制图像"""
def use_svg_display(): #@save
    """使⽤svg格式在Jupyter中显⽰绘图。"""
    matplotlib_inline.backend_inline.set_matplotlib_formats('svg')
    """下面这个函数在3.7以后都被废弃了，没啥用，别用了替换成上面这个"""
    #display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)): #@save
    """设置matplotlib的图表⼤⼩。"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴。"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
        ylim=None, xscale='linear', yscale='linear',
        fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点。"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()
    # 如果`X` 有⼀个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
            and not hasattr(X[0], "__len__"))
    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
d2l.plt.show()

注意，注释#@save是⼀个特殊的标记，会将对应的函数、类或语句保存在d2l包中因此，以后⽆须重新定义
就可以直接调⽤它们（例如，d2l.use_svg_display()）。

7.梯度

参考文章网址：

https://zh-v2.d2l.ai/chapter_preliminaries/calculus.html

第一个和第二个有点迷


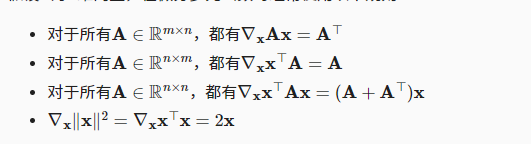
8.自动求导

​ 深度学习框架通过⾃动计算导数，即⾃动求导（automatic differentiation），来加快这项⼯作。实际中，根据我们设计的模型，系统会构建⼀个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产⽣输出。⾃动求导使系统能够随后反向传播梯度。这⾥，反向传播（backpropagate）只是意味着跟踪整个计算图，填充关于每个参数的偏导数。

x=torch.arange(4.0)
"""注意一定要加这个.0"""
print(x)
x.requires_grad_(True)
print(x)
print(x.requires_grad_(True))
print(x.grad)
y=2*torch.dot(x,x)
print(y)
"""计算y关于x的梯度"""
y.backward()
print(x.grad)
"""由于x会积累梯度，所以需要清楚之前的值"""
x.grad.zero_()
print(x.grad)

"""非标量向量的反向传播"""
y=x*x
print(x)
y.sum().backward()
print(x.grad)

"""分离计算：
假设y是x的函数
z是y和x的函数
假设z=y*x
y=x**2
但是我只需要考虑z关于x的偏导，而不考虑y的影响的时候使用
这时候y是一个常数
"""
x.grad.zero_()
y=x*x
u=y.detach()
"""u的意思是获得一个与y等值的常数张量"""
z=u*x
print(u)
z.sum().backward()
print(x.grad)
x.grad.zero_()
y.sum().backward()
print(x.grad)

"""python控制流的梯度计算"""
"""
定义f1的分段函数，对于f1来说，根据条件不同
式子也不同

"""

9.概率

iterable：可迭代的

概率这个东西吧，涉及到大量算法

这一小节了，先实现一些显示计算的东西，这里的一些写法可以用于遗传算法的轮盘赌

"""概率"""
fair_probs=torch.ones([6])*7
"""为什么要除以6，改过后没啥区别啊"""
print(fair_probs)
cc=multinomial.Multinomial(1000,fair_probs).sample()
"""注意，这个函数不是返回0-1000的随机数，而是统计6个位置，每个位置随机出现的次数的综合
比如实验次数为1000，那么就是这个矩阵中所有数据出现的次数之和为1000"""
print(cc/1000)
"""multinomial.Multinomial(实验次数,输入矩阵).sample(实验场数)"""
counts=multinomial.Multinomial(10,fair_probs).sample((500,))
print(counts)
cum_counts=counts.cumsum(dim=0)#对列方向进行累加
print(cum_counts)
estimates=cum_counts/cum_counts.sum(dim=1,keepdims=True)
"""按照行进行相加，keepdims is iterable flag,if iterable is equal to 1,the value will iterable according to dim """
print(estimates)
print(cum_counts.sum(dim=1,keepdims=True))
d2l.set_figsize((6,4.5))
for i in range(6):
    d2l.plt.plot(estimates[:,i].numpy(),label=("P(die="+str(i+1)+")"))
d2l.plt.axhline(y=0.167,color='black',linestyle='dashed')
d2l.plt.gca().set_xlabel('实验次数')
d2l.plt.gca().set_ylabel('估算概率')
d2l.plt.legend()
d2l.plt.show()

10查询功能

import torch
print(dir(torch.distribution))
"""这样就会打印一堆这里面的函数"""