基于高斯掩膜的质心定位算法

1.参考文献地址

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6163372/#:~:text=The Gaussian fitting algorithm (GF) is the most,the experiments are carried on the MATLAB

2.算法与仿真

a.传统质心定位算法

$(x_c,y_c)=(\frac{\sum_iI_ix_i}{\sum_iI_i},\frac{\sum_iI_iy_i}{\sum_iI_i})$

matlab代码实现：

clc;
close all;
clear all
img=imread('test.png');
img=rgb2gray(img);
img=double(img);
c=sum(sum(img));
[m,n]=size(img);
aa=(1:1:m);
dd=aa*img;
y_c=sum(dd)/c;
bb=(1:1:n)';
x_c=sum(img*bb)/c
figure
    set(gcf,'color','w');
    imshow(img,[])
    hold on
    plot(x_c,y_c,'*','MarkerSize',10,'MarkerEdgeColor','r')
  

b.高斯光质心定位

参考博客：

https://blog.csdn.net/dedell/article/details/107960123

我们认为接收的光强组成式子如下：

$I_i=S_i+N_i$

$其中S_i为光源物体发出来的有效光，N_i为背景噪声，I_i为观测光强$

其中我们认为星点类光源接收到的光，满足高斯分布，我们也大致认为，波前传感器接收到的光强满足高斯分布，分布公式如下面式子所示：

$S(x_i,y_i|v)=Aexp(-\frac{(x_i-x_c)^2}{2\sigma_x^2}-\frac{(y_i-y_c)^2}{2\sigma_y^2}) \\ \sigma_x与\sigma_y为标准差，A为光强，x_i,y_i为图像坐标，x_c,y_c为被计算质心 \\ 如何确定\sigma_x\sigma_y为主要研究对象$

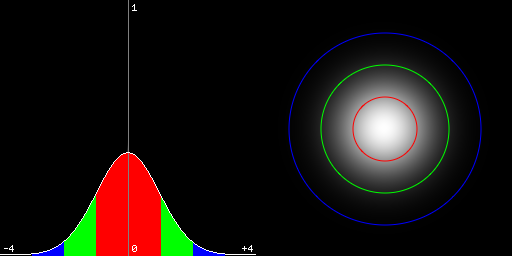
使用快速高斯质心定位算法，其核心公式为：

$\left\{ \begin{aligned} m=\frac{1}{2\sigma_x^2}\\ n=\frac{1}{2\sigma_y^2}\\ p=-\frac{x_c}{\sigma_x^2}\\ q=-\frac{y_c}{\sigma_y^2}\\ k=\frac{x_c^2}{2\sigma_x^2}+\frac{y_c^2}{2\sigma_y^2}-InA\\ \end{aligned} \right.$

$h_i=mI_ix_i^2+nI_iy_i^2+pI_ix_i+qI_iy_i+kI_i+I_iInI_i$

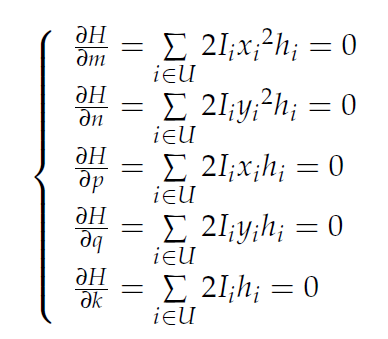
matlab代码实现

clc;
close all;
clear all

img=double(rgb2gray(imread('test.png')));
k=abs(fftshift(fft2(img)));
img=img;
figure
imshow(k,[])
[m,n]=size(k);
figure
 plot(1:m,k(:,n/2))
 figure
 imshow(img,[])
 m1=linspace(0,m,m);
 n1=linspace(0,n,n);
 [m2 n2]=meshgrid(n1,m1);
 I_ix_i2=img.*(m2.^2);
 I_iy_i2=img.*(n2.^2);
 I_ix_i=img.*(m2);
 I_iy_i=img.*(n2);
 I_i=img;
 where=find(img==0);
 bb=img.*log(img);
 bb(where)=0;
 %% 写这么丑的原因使因为这样子好看原理
 aaaa=[sum(I_ix_i2(:).^2)           sum(I_ix_i2(:).*I_iy_i2(:) ) sum(I_ix_i2(:).*I_ix_i(:))  sum(I_ix_i2(:).*I_iy_i(:))  sum(I_ix_i2(:).*img(:));
       sum(I_ix_i2(:).*I_iy_i2(:))  sum(I_iy_i2(:).^2 )          sum(I_iy_i2(:).*I_ix_i(:))  sum(I_iy_i2(:).*I_iy_i(:))  sum(I_iy_i2(:).*img(:));
       sum(I_ix_i2(:).*I_ix_i(:))   sum(I_ix_i(:).*I_iy_i2(:) )  sum(I_ix_i(:).*I_ix_i(:))   sum(I_ix_i(:).*I_iy_i(:))   sum(I_ix_i(:).*img(:));
       sum(I_ix_i2(:).*I_iy_i(:))   sum(I_iy_i(:).*I_iy_i2(:) )  sum(I_ix_i(:).*I_iy_i(:))   sum(I_iy_i(:).*I_iy_i(:))   sum(I_iy_i(:).*img(:));
       sum(I_ix_i2(:).*I_i(:))      sum(I_i(:).*I_iy_i2(:) )     sum(I_i(:).*I_ix_i(:))      sum(I_i(:).*I_iy_i(:))      sum(I_i(:).*img(:));];
 bbbb=-[sum(I_ix_i2(:).*bb(:))
       sum(I_iy_i2(:).*bb(:))
       sum(I_ix_i(:).*bb(:))
       sum(I_iy_i(:).*bb(:))
       sum(I_i(:).*bb(:))];
   cccc=mldivide(aaaa,bbbb);
   x_c=-cccc(3)/cccc(1)/2
   y_c=-cccc(4)/cccc(2)/2
   t_x=1/sqrt(2*cccc(1))
   figure
    set(gcf,'color','w');
    imshow(img,[])
    hold on
    plot(x_c,y_c,'*','MarkerSize',10,'MarkerEdgeColor','r')

高斯拟合法比灰度质心定位法好很多，这里随机了一百个质心偏移的点，最后误差结果如图所示